[Python] CodeSignal 문제 풀이 (49~51)
2020. 4. 14. 17:02ㆍPython/CodeSignal Algorithm
49. Given a string, return its encoding defined as follows:
- First, the string is divided into the least possible number of disjoint substrings consisting of identical characters
- for example, "aabbbc" is divided into ["aa", "bbb", "c"]
- Next, each substring with length greater than one is replaced with a concatenation of its length and the repeating character
- for example, substring "bbb" is replaced by "3b"
- Finally, all the new strings are concatenated together in the same order and a new string is returned.
[Example]
| For s = "aabbbc", the output should be lineEncoding(s) = "2a3bc". |
[Solution]
#<My Code>
def lineEncoding(s):
l = []
cnt = 1
c = ""
result = ""
for i in range(len(s)):
if i == 0:
c = s[0]
continue
if c == s[i]:
cnt += 1
else:
if cnt == 1:
result += c
else:
result += str(cnt) + c
c = s[i]
cnt = 1
if cnt == 1:
result += c
else:
result += str(cnt) + c
return result
#<Best Code>
from itertools import groupby
def lineEncoding(s):
x = ''
for k,g in groupby(s):
y = len((list(g)))
if y==1:
x += k
else:
x += str(y) + k
return x
50. Given a position of a knight on the standard chessboard, find the number of different moves the knight can perform.
The knight can move to a square that is two squares horizontally and one square vertically, or two squares vertically and one square horizontally away from it. The complete move therefore looks like the letter L. Check out the image below to see all valid moves for a knight piece that is placed on one of the central squares.

[Example]
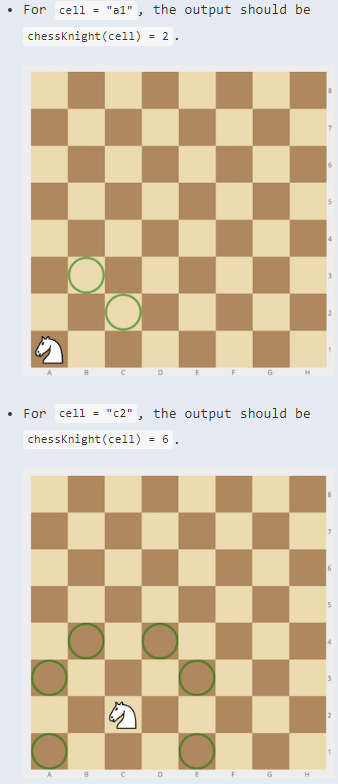 |
[Solution]
#<My Code>
def chessKnight(cell):
a, n = cell[0], cell[1]
#<Best Code>
51. Given some integer, find the maximal number you can obtain by deleting exactly one digit of the given number.
[Example]
|
[Solution]
#<My Code>
def deleteDigit(n):
strN = str(n)
maxDigit = 0
for i in range(len(strN)):
num = 0
if i == 0:
num = int(strN[1:])
elif i == len(strN) - 1:
num = int(strN[:-1])
else:
num = int(strN[0:i] + strN[i + 1:])
if maxDigit < num:
maxDigit = num
return maxDigit
#<Best Code>
def deleteDigit(n):
n = str(n)
return max(int(''.join(n[:i]+n[i+1:])) for i in range(len(n)))'Python > CodeSignal Algorithm' 카테고리의 다른 글
| [Python] CodeSignal 문제 풀이 (55~57) (0) | 2020.04.27 |
|---|---|
| [Python] CodeSignal 문제 풀이 (52~54) (0) | 2020.04.14 |
| [Python] CodeSignal 문제 풀이 (46~48) (0) | 2020.03.31 |
| [Python] CodeSignal 문제 풀이 (43~45) (0) | 2020.03.31 |
| [Python] CodeSignal 문제 풀이 (40~42) (0) | 2020.03.31 |